The main purpose of the simulation subsystem is to apply different planning and scheduling methods to prove the effectiveness of collaboration in selecting optimal parking policies for more than a hundred vehicles arriving and exiting at random instances of time. Through collaboration between vehicles, it is possible to have efficient planning and scheduling to optimize the parking process. The main objectives being minimized are average parking time, average pause time and average exit time. To give some context to the entire subsystem implementation, following are videos of the simulation environment comparing a simple greedy approach (first empty spot) and the optimized approach.
Greedy
Optimized
Working:
The working of the simulation system can be understood in as follows. The simulation system is initiated whenever a vehicle enters the parking lot in the visualization. The new car is added to a queue and the rendering engine queries the global planner regarding which spot should be designated to the new entrant. The global planner receives information regarding the current state of the all the spots in the lot and uses this information to update the cost of each spot in the parking lot. After this update, the global planner queries the local planner regarding costs of specific spots. This query is needed to take into account the cost to reach a spot given the current condition of the parking lot. The local planner returns the cost associated with the spot and the global planner uses this to find the best spot in the parking lot. This information is relayed to the rendering engine. The rendering engine, having received the spot the car in the queue should park at, queries the local planner for a path to reach that spot. The local planner returns a path to the rendering engine which is used to park the car in the designated spot.
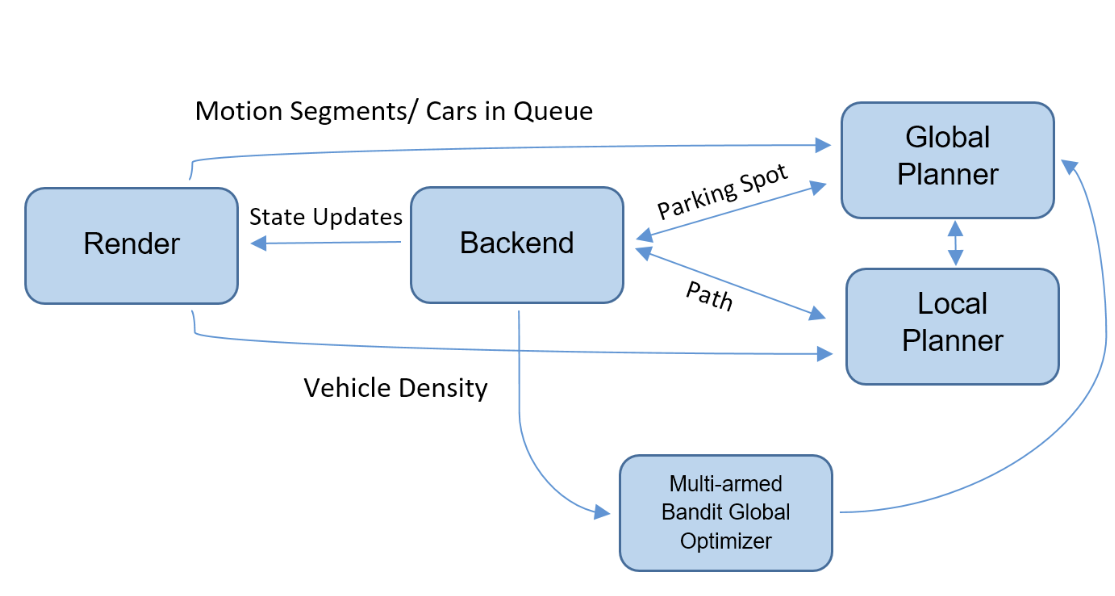
The simulation subsystem was implemented using ROS and the detailed simulation architecture is shown in the figure below:
Figure 2: Detailed software architecture of simulation subsystem
The simulator was divided into four major sections whose details are specified below:
- Global Planner: This planner is responsible to rank and assign costs to parking spots based on multiple heuristics. The decision to assign a spot to the car is made by this unit. This information is then relayed to the simulation engine to be processed and rendered in the environment. This planner takes into account the static costs base of a spot in the parking lot (distance to exit, nearby occupied spots) as well as the dynamically changing costs associated with selecting a spot (cost to navigate to the spot, cars in queue and time of the day). SBPL’s ARA* is being used for implementation of distance to exit heuristic.
- Local Planner: It is a custom Astar lattice based planner for planning in continuous state space of the robot i.e x,y, and heading. It returns a path and path cost for a query from either the rendering engine or global planner which consists of a start and end pose. The planner takes into account the distance from obstacles while planning and uses an ackerman steering motion model for motion primitives with sixteen different motion primitives consisting of steering and distance control inputs. Using these primitives continuous car-like motions can be generated. The planner relays a dynamic cost to the global planner associated with navigating to a spot. It relays a path to the rendering engine between the queried points.
Assumptions/Drawbacks
Using just the above two planners, better results can be obtained than a simple greedy approach of choosing the first empty spot. But, during tests it was found that there are many assumptions and drawbacks of the deterministic optimization approach such as:
- The entry and exit of vehicles is a random process and hence the rewards obtained are random. The heuristic based optimization does not take this into account and optimizes only based on the current state of the parking lot. Thus, it is easy to get stuck in locally optimal solutions.
- Due to only exploitation of good “areas” of the large motion density is seen in those areas which affects the average park time, pause time and exit time.
The third component of the simulation system helps overcome this drawback.
- Multi-Armed Bandit (mab) Planner: In order to generate a globally optimal policy for parking vehicles, a trade-off between exploration and exploitation is required. Also, the heuristic based planner does not take into account the random process of arrival and exit of vehicles. Hence, a multi-armed bandit approach was employed which uses UCB1 arm pulls as a one step look-ahead policy. To implement this, the parking lot is divided into four different areas and each area is evaluated on the actual average time to park and exit in the area . Whenever a car enters the parking lot, it is assigned a one-step lookahead based on a UCB1 policy after which the default heuristic policy is followed in that area. When the car parks or exits, the statistics for that area are updated. Since the distribution is non-stationary, a discounted approach is employed. This online planning helps to significantly improve the park, pause and exit times. The formulation of UCB1 for the parking garage problem is shown below.
At every time step n, an action ‘a’ is chosen according to the following formula
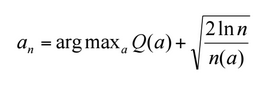where, Q(a) is the current average time to park and exit in a particular area averaged over the number of spots.
n(a) is the number of times that particular area has been chosen till now.How this approach is better
- Performs better than greedy and deterministic planning approaches when simulated for longer periods of time(which is feasible for parking lots!)
- No additional load on communication.
- Still Decentralized.
- Totally General and scalable approach.
- Rendering Engine: It accepts the data from other nodes to render an environment showing the state of all the vehicles in the parking lot. RVIZ markers are used for the visualization of different vehicles and their paths. It also updates the other systems with the real-time state of the lot so that planning can take the dynamic environment into account. The rendering engine also run a Numerical Optimization to switch places of cars based on a trade off between cost minimization and reward maximization. The cost in this case is the addition to entropy of the system and the reward is reduction in return times.
Figure 3: The simulation system in action
Results
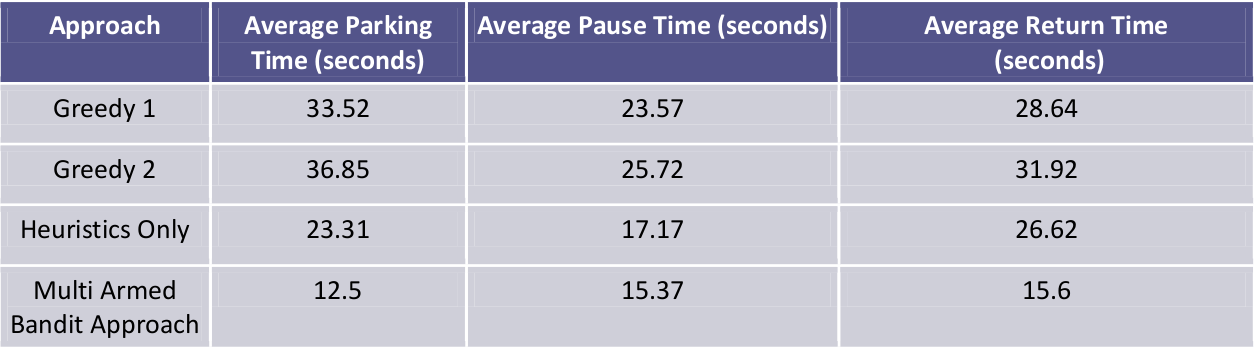
The performance of our planner and the greedy first-spot approach (Greedy 1) and closest spot to exit (Greedy 2) were compared in the simulation environment. In our planner, the heuristics only and multi-armed bandit approach were tested. The approaches were compared based on three criteria- average time to park, average time to exit and the average pause time of each vehicle. The average pause time denotes the time a vehicle stops inside the parking lot due to congestion. Minimizing each of these times reflects a good planning strategy, as can be seen in the figure below.
Figure 4: Results obtained using different planning approaches